Game, Set and Fuzzy match

Written by Bhargav Bharadwaj, Antoine Gracia Victoria, Wiktor Owczarz and Waldemar Schuppli

Fuzzy matching is a set of data science techniques that save critical time and reduce the risk of human error when matching string variables (e.g., customer names) in large, distinct datasets, for example, to assess the closeness of competition between merging firms, or to calculate market shares.

Matching names in distinct datasets is challenging

We often need to combine information from multiple distinct datasets. In a merger case for instance, to assess closeness of competition between the merging firms, we may need to combine their respective customer lists to assess how many of their customers they have in common. Or, to calculate market shares, we may need to combine data from the merging firms with external third-party data.

Such a mapping exercise, however, can be challenging for many reasons, including but not limited to:

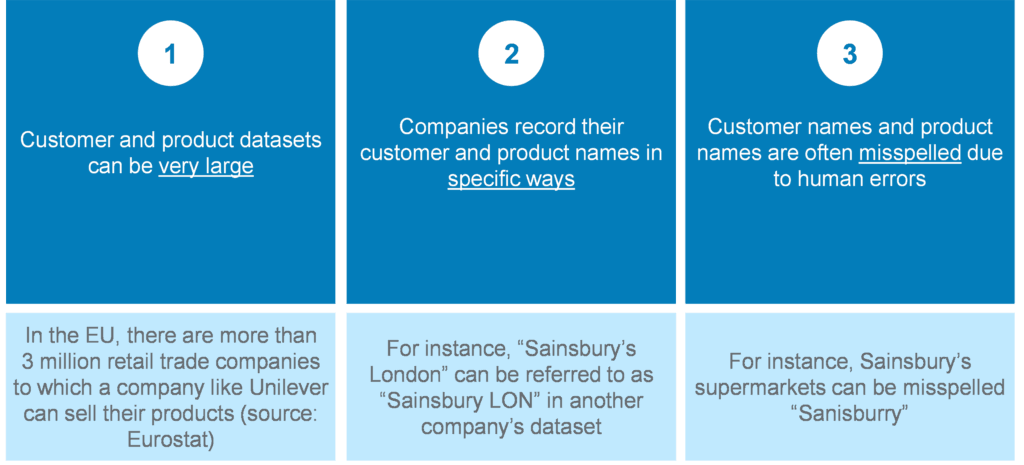
This exercise is traditionally performed by manually inspecting the lists and identifying matches based on “intuition”. For smaller datasets, near-perfect results can be achieved this way, although it is time-consuming. For larger datasets, manual inspection is very challenging - if not impossible when deadlines are tight – with a high risk of manual errors.

How can we improve on this manual approach? Using a set of techniques known as “fuzzy matching”, [1] we automate most of the work, allowing more time to be spent on substantive analysis.

Solving this challenge with fuzzy matching algorithms

The basis of fuzzy matching is to take two sequences of characters (two “strings”) and calculate a similarity score between 0 and 1, based for instance on the number of characters they have in common. The more similar two strings are, the closer their similarity score will be to 1.

Two of the most common algorithms are the Jaro-Winkler similarity score and the Cosine similarity score, which share the same end-goal but differ in the approach.[2]

Jaro and Jaro-Winkler similarity scores

Jaro similarity is an edit-distance based score. The Jaro similarity score collects all characters two strings have in common[3] and, within these two sets of matched characters, computes the number of transpositions (changes of character’s place) required for them to become identical. The fewer the number of transpositions needed, the higher the similarity score.

According to this algorithm, “Example” and “Exmaple” will be very similar as it only requires one transposition to make them identical.

The following video calculates the Jaro similarity score between “Sainsbury” and a misspelled “Sanisburry”.

In practice, we often use a variant - the Jaro-Winkler similarity score - which penalizes differences near the beginning of the string more than it penalizes those at the end of it[4] since spelling errors occur more frequently at the end of a string than at the beginning[5].

Cosine similarity score

Cosine similarity is an n-gram based approach. It splits strings into subsets (“grams”) of either 1 character (unigrams), 2 characters (bigrams), etc. For example, “RECURRENCE” can be split into the following bigrams: {RE, EC, CU, UR, RR, RE, EN, NC, CE}. The more grams two strings have in common, the higher the similarity score.[6]

The following video calculates the Cosine similarity score between “Sainsbury” and a misspelled “Sanisburry”, using bigrams.

Pros and cons of Jaro-Winkler and Cosine similarity scores

There are many string-matching algorithms. Expertise and experience are indispensable to determine which algorithm to apply to each specific situation.

Jaro-Winkler similarity performs better on misspelled strings. On the other hand, Cosine similarity score is based on “simpler” calculations than Jaro-Winkler[7], hence is more scalable, which means it works faster on very large datasets. When comparing longer strings, where words can be swapped (e.g., name, surname vs. surname, name), Cosine similarity could be more appropriate as it does not consider the order in which words appear.

In practice, we often use multiple algorithms and compare or combine their results.

The need for human supervision

Fuzzy matching algorithms, and data science more generally, is not a magic bullet to solve data-related challenges without human supervision.

For instance, users must tailor to their own specific project the threshold above which two strings will be considered as a match:

On the contrary, a high threshold will minimize the inspection of false positives but is likely to lead to more false negatives.

Fuzzy matching is easily accessible on all our projects

In principle, one would need some programming skills to perform fuzzy matching, ideally in Python, to manage a long list of tasks.[8] However, for most matching tasks, things don’t need to be so complicated.

At Compass Lexecon, we have standardized these algorithms into an off-the-shelf tool that is used by our economists. Not only does it mean that such techniques are accessible easily on all our projects, but it also allows our data scientists to improve continually the “back-end”, adding more algorithms and functionality.

Fuzzy matching in a recent merger case

In a recent global merger case, we had to identify which of the merging firms’ customers could be considered as “large” customers. This involved checking the Parties’ datasets against a third-party data source of all companies with revenue above a certain threshold.

The task involved checking close to 500,000 customer names from the Parties against a list of about 250,000 company names. Given the magnitude of this task, as well as its tight deadline (two weeks), it was infeasible to overcome with manual inspection.

Indeed, if it takes one minute to search through the Parties’ datasets to find (or not) a company name in the third-party dataset, it would have taken over 8,000 hours to complete.

Instead, we used the Compass Lexecon’s fuzzy matching tool. Given the size of the datasets, we primarily used the Cosine similarity score, with checking results against the Jaro-Winker similarity score on subsets of the data. This allowed us to complete the task well ahead of the deadline.

Final word

The Compass Lexecon Data Science team was created to bring the latest developments in programming, machine learning and data analysis to economic consulting.

Sometimes this involves applying novel techniques to assess specific questions in an innovative and compelling way. For instance, running a sentiment analysis on social media content related to merging firms can be informative on their closeness of competition, and can supplement the results of a survey.

Other times it is about making work faster, more accurate, and more efficient, especially on cases which involve large datasets.

In the case of fuzzy matching, the Compass Lexecon Data Science team:

Trained people on how to use this tool, especially on the need for human supervision.

This short article is the first of a series of articles we will publish in the coming months, showcasing how data science can lead to more streamlined and robust economic analysis and ultimately to better decisions in competition cases. If you would like to find out more, please do not hesitate to reach out to us at datascience@compasslexecon.com.

---

[1] Fuzzy matching is also referred to as record linkage. It belongs to a wider domain called entity resolution, which aims to disambiguate records within and across datasets. In addition to record linkage. Entity recognition includes other tasks such as deduplication, canonicalization and referencing. 

[2] Other commonly used algorithms include Levenshtein distance or Soundex. In this article, we focus on Jaro-Winkler and Cosine similarity, due to their properties, explained below.

[3] In practice, the algorithm compares each character in one string to a range of characters in the other string. Therefore, it is not restricted by the order in which the same character appears in the two strings. It allows to a certain extent to account for misspelled words, but two identical characters must not be too far apart in the two strings to be considered a match.

[4] Find further details here. 

[5] J. J. Pollock and A. Zamora. Automatic spelling correction in scientific and scholarly text. Communications of the ACM, 27(4):358–368, 1984.

[6] Find further details here. 

[7] Cosine similarity is essentially a matrix multiplication problem, whereas Jaro-Winkler similarity requires a pairwise comparison of each string.

[8] Pre-processing the strings in the datasets (converting to Unicode), cleaning the string names (removing special characters, legal entity names), managing memory allocation, parallelising the processes… the list goes on.